Определение площади земельного участка. Методы и погрешности
При проведении землеустроительных работ используются различные способы вычисления площадей участков земли. Применение этих способов зависит от ценности этих участков, их величины, формы границ, наличия и точности данных измерений на местности, наличия карт необходимой точности и планов участков.
СодержаниеПоказать
Основные способы
Существует три основных способа определения площадей:
- аналитический;
- графический;
- механический.
Для графического способа используются данные измерений на плане и карте.
Такой способ чаще всего используется при отсутствии информации полевых измерений.
При механическом способе площадь определяется по плану с помощью специального устройства — планиметра.
Иногда используется комбинированный способ определения площади. Например, общая площадь участка определяется по координатам характерных точек аналитическим способом, а площади внутренних участков определяются по плану с помощью графического или механического методов.
Эти три метода имеют различные показатели точности.
Наиболее точным является аналитический метод. На точность этого метода влияют только погрешности полевых измерений.
Точности других методов, использующих топографическую информацию с планов, зависят еще и от погрешностей приборов, качества плана, масштаба, деформации бумаги.
Аналитический способ
Аналитический способ позволяет по координатам характерных точек границ участка определить его площадь. При этом используются формулы аналитической геометрии.
В соответствии с ними площадь многоугольника S может быть определена по формуле:
S= 0,5*∑(Xi*(Yi+1-Yi-1), где:
- Xi и Yi — координаты i-той характерной точки участка, имеющего вид многоугольника;
- i — порядковый номер характерной точки ЗУ.
 Этот параметр меняется от 1 до n;
Этот параметр меняется от 1 до n; - n — число характерных точек.
Если участок имеет четырехугольную форму, то, в общем случае, для него расчет площади производится по приведенной выше формуле с учетом того, что n=4.
Если участок имеет форму трапеции и известны его стороны, то площадь такого участка можно определить по формуле:
Sт=0,5*(a+b)*h, где:
- a и b — основания фигуры;
- h – высота трапеции.
При расчете четырехугольника неправильной формы, когда известны размеры его сторон, вначале определяют величину полупериметра p:
р=0,5(а+B+c+d), где:
a,b,c,d — величины сторон.
Тогда площадь участка Sу будет равна:
Sy=√(p-a)(p-b)(p-c)(p-d).
В некоторых случаях, когда имеется много точек поворота, аналитический расчет площади участка производится с использованием данных об углах азимута.
При этом по контуру границ участка производится замер азимута каждой характерной точки. Также определяется расстояние от одной характерной точки до следующей за ней точки. Вся эта информация в дальнейшем вводится в ЭВМ, которая по специальной программе производит расчет площади ЗУ.
Также определяется расстояние от одной характерной точки до следующей за ней точки. Вся эта информация в дальнейшем вводится в ЭВМ, которая по специальной программе производит расчет площади ЗУ.
Графический метод
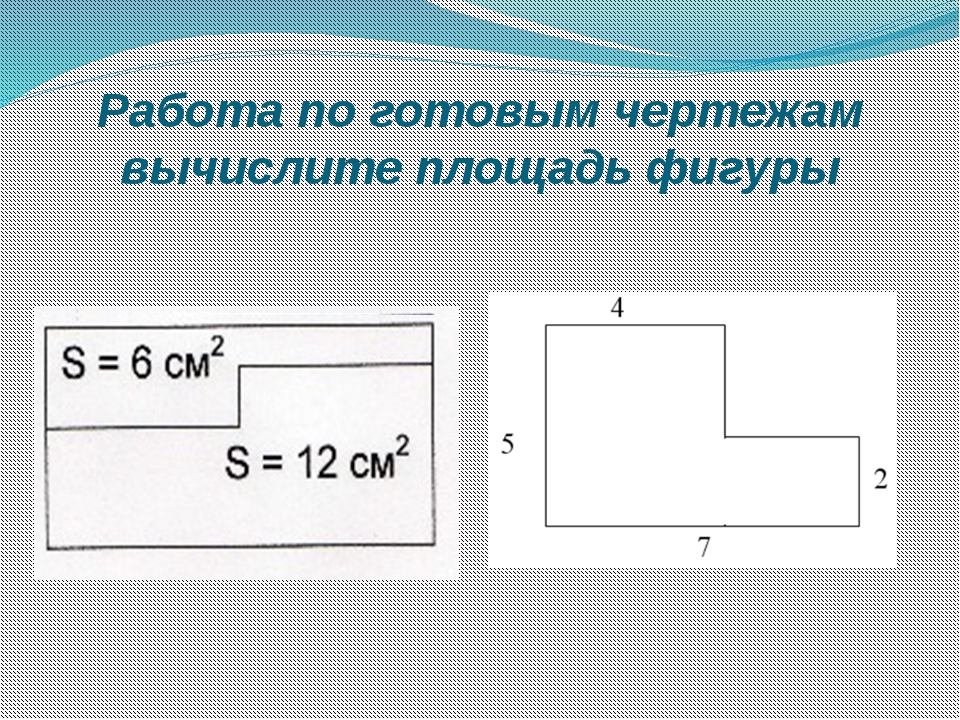
При расчете площади участка графическим методом чаще всего изображенный на плане участок сложной формы делят на участки элементарного вида (треугольники, прямоугольники, трапеции), затем вычисляют и суммируют площади этих фигур.
Точность графического метода зависит от точности графического измерения на плане. Известно, что точность измерения с помощью циркуля постоянна и равна 0,1 мм. Поэтому относительная ошибка при измерении коротких линий больше, чем при измерении длинных линий. В связи с этим желательно, чтобы простые фигуры были больших размеров и с близкими по размерам основаниями и высотами.
Такой метод удобен в случае, когда имеется небольшое количество характерных точек. В противном случае целесообразнее определять площадь участка по координатам точек, измеренных на плане.
В некоторых случаях участки имеют криволинейную форму, которую трудно аппроксимировать простыми фигурами. В таких случаях могут использоваться палетки.
Палетка представляет собой прозрачный лист, на который нанесены деления. Этот лист накладывается на план участка. Сосчитав количество делений, входящих в контур участка, и определив площадь одного деления с учетом масштаба, можно оценить площадь участка.
Недостаток такого графического метода состоит в том, что количество неполных квадратов приходится оценивать на глаз. В результате этого ухудшается точность данного метода.
Механический способ
Механический способ используется в тех случаях, когда по плану необходимо оценить площадь большого участка со сложными границами. Для осуществления этого метода используются планиметры.
Планиметр представляет собой прибор, который позволяет определить площадь плоской фигуры путем обвода ее контура. Он состоит из двух рычагов и каретки со счетным механизмом.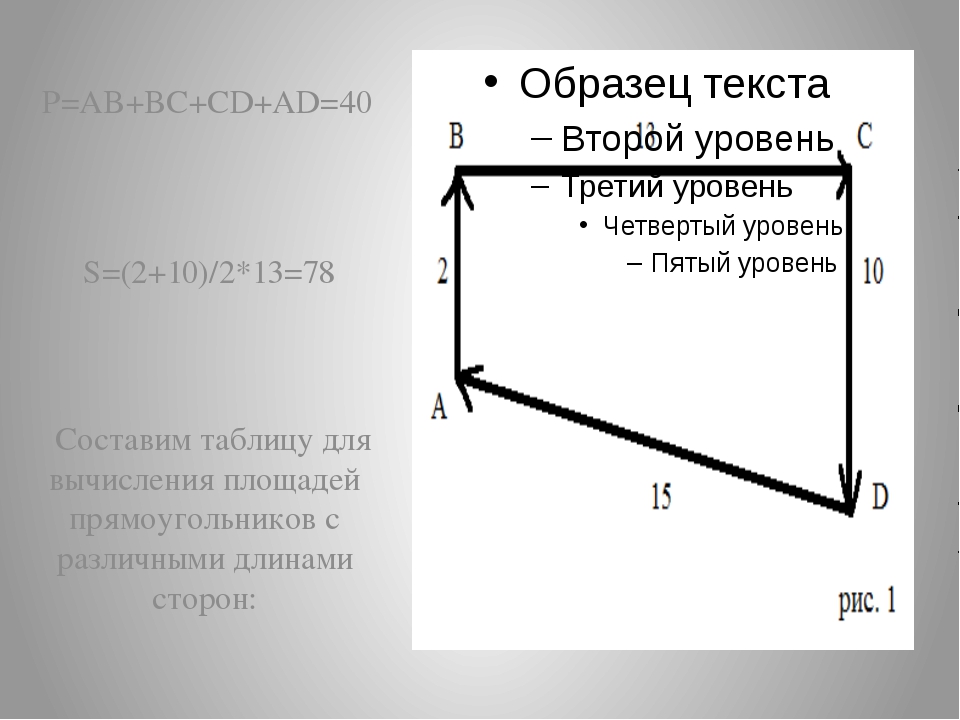 На полюсном рычаге имеется игла, которая втыкается в план и является полюсом. Вокруг полюса по контуру участка движется обводной шпиль.
На полюсном рычаге имеется игла, которая втыкается в план и является полюсом. Вокруг полюса по контуру участка движется обводной шпиль.
Точность метода зависит от размеров участка и свойств плана.
Погрешность определения площади
При определении площадей участков возникают неточности, которые характеризуются погрешностями. Погрешность — это разность между вычисленной величиной площади участка и ее истинной величиной.
Для различных методов определения площади такие погрешности могут быть различными.
Для аналитического метода точность расчета площади зависит исключительно от погрешностей, связанных с измерением координат поворотных точек. При этом, средняя квадратическая погрешность (СКП) аналитического метода расчета (mp) определяется формулой:
mp= mt*√ P, где:
- mt — СКП расположения поворотных точек;
- P — площадь участка.
Для примера можно взять допустимые при межевании точности mt, которые определены соответствующими нормативными актами (например, Приложением к приказу МЭР № 518). Эти точности зависят от типа земель.
Эти точности зависят от типа земель.
Так, для населенных пунктов этот показатель равен 10 см, а для дачных участков и садоводств-20 см. Таким образом, для садового участка в 600 кв. м точность определения площади аналитическим методом может составить:
mpс= 0,2*√600=4,89 м.
При реализации графического метода на его точность влияют погрешности измерений, погрешности составления плана, деформация бумаги. Относительная погрешность такого метода составляет от 1:500 до 1:1000.
Точность механического метода также зависит от погрешностей составления плана (или карты), состояния бумаги, на которой нанесен план участка. Кроме того, на точность этого метода влияет размер участка. Этот метод не рекомендуется применять для участков размером менее 10-12 см2.
В благоприятных условиях относительная погрешность измерений площади планиметром может достигать 1:400.
Определение площади участка на ПКК
Публичная кадастровая карта (ПКК) — это онлайн-сервис, с помощью которого любой гражданин может узнать основные характеристики любого земельного участка, помещенные в кадастр недвижимости (ЕГКН).
Для того, чтобы узнать величину площади с помощью ПКК, надо зайти на страницу http://pkk5.rosreestr.ru и найти участок на карте. Для этого используется специальное меню, которое позволяет определить участок по кадастровому номеру, адресу.
Так, введя в поисковую систему ПКК адрес участка, можно получить его расположение на карте и некоторые данные.
Среди этих данных имеется площадь данного участка, которая является официальной величиной, так как она введена в ЕГРН.
Необходимо отметить, что не все участки земли можно таким образом найти по адресу. Например, при нахождении участка c кадастровым номером 50:38:0050302:130 в таблице его параметров указан адрес: «обл. Московская, р-н Зарайский, снт «Изобретатель», уч-к 116″.
Однако при обращении к ПКК с использованием этого адреса система дает сбой. Подобный результат получается и при обращении к ПКК на других страницах.Это говорит о том, что система поиска земельного участка на ПКК по адресу не до конца отработана Росреестром.
Чтобы определить площадь участка по координатам, вначале необходимо узнать эти координаты. Если участок уже найден на карте, то приблизительные координаты характерных точек можно определить, подводя к ним курсор. По этим координатам, в дальнейшем, можно определить площадь участка по формуле для аналитического метода.
Более точно координаты характерных точек участка можно узнать только при платном заказе выписки из ЕГРН для этого участка.
По новому закону в связи с объединением баз данных ЕГРП и ЕГРН такая выписка с 1.01 2017 года заменяет собой свидетельство на объект недвижимости, кадастровый паспорт, кадастровую выписку и выписку из ЕГРП. То есть, выписка из ЕГРН является основным документом на недвижимость.
Не нашли ответа на свой вопрос? Звоните на телефон горячей линии 8 (800) 350-34-85.Это бесплатно.
Юрист. Практика в сфере недвижимости, тудового права, семейного права, защите прав потребителей
Площадь четырехугольника
Площадь произвольного четырехугольника
В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.
Таблица с формулами площади четырехугольника (в конце страницы)
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)
1
Площадь четырехугольника по диагоналям и углу между ними
. .. подготовка …
.. подготовка …
d1 — диагональ
d2 — диагональ
α° — угол между диагоналями
2
Площадь четырехугольника через стороны и углы между этими сторонами
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
… подготовка …
a — сторона
b — сторона
c — сторона
d — сторона
α° — угол между сторонами
β° — угол между сторонами
3
Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты
Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
… подготовка …
a — сторона
b — сторона
c — сторона
d — сторона
4
Площадь четырехугольника в который можно вписать окружность
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
… подготовка …
a — сторона
b — сторона
c — сторона
d — сторона
r — радиус вписанной окружности
5
Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность.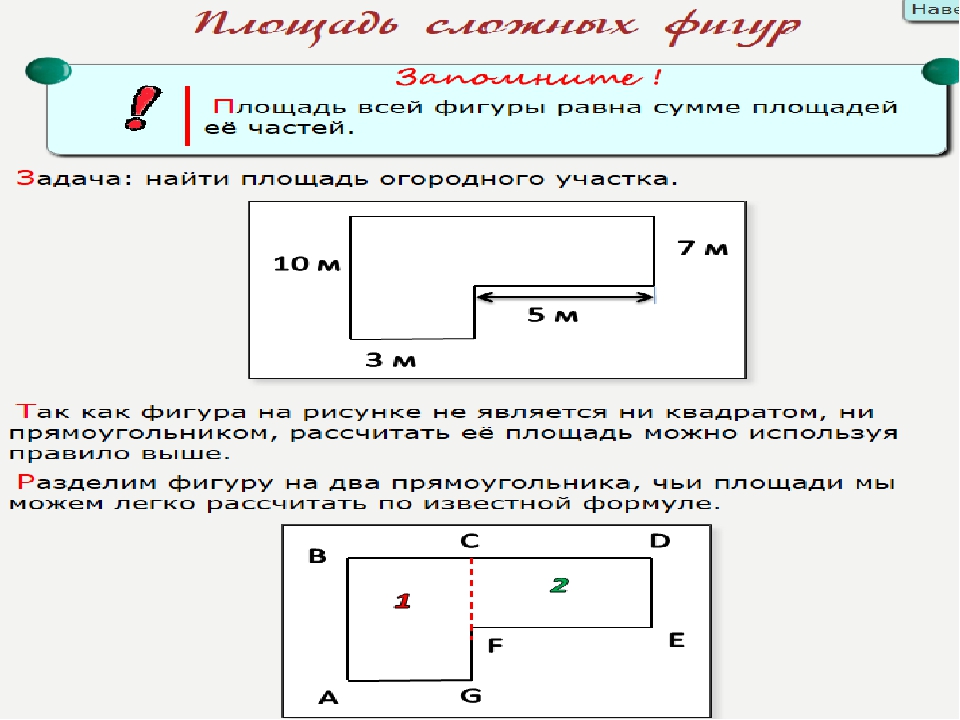 Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
… подготовка …
a — сторона
b — сторона
c — сторона
d — сторона
α° — угол между сторонами
β° — угол между сторонами
Примечание:
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади четырехугольника
Площадь частных случаев четырехугольников
Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:
Определения
Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь четырехугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Площадь прямоугольника
Площадь прямоугольника, формулы для вычисления площади прямоугольников в зависимости от известных исходных данных, калькулятор для нахождения площади онлайн и сводная таблица с формулами площадей прямоугольника. Наш калькулятор поможет вам бесплатно в режиме онлайн вычислить площадь прямоугольника с помощью различных формул или проверить уже выполненные вычисления.
Таблица с формулами площади прямоугольника (в конце страницы)
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)
1
Площадь прямоугольника через две стороны
. .. подготовка …
.. подготовка …
a — сторона
b — сторона
2
Площадь прямоугольника через периметр и одну из сторон
В указанной формуле, площадь периметра прямоугольника вычисляется:
… подготовка …
a (или
P — периметр
3
Площадь прямоугольника по диагонали и стороне
… подготовка …
a (или b) — сторона
d — диагональ
4
Площадь прямоугольника по диагоналям и углу между ними
… подготовка …
d — диагональ
α° — угол между диагоналями
5
Площадь прямоугольника через сторону и радиус описанной окружности
. .. подготовка …
.. подготовка …
a (или b) — сторона
R — радиус описанной окружности
6
Площадь прямоугольника через сторону и диаметр описанной окружности
… подготовка …
a (или b) — сторона
D — диаметр описанной окружности
Примечание:
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади прямоугольника
Определения
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Площадь треугольника
Площадь треугольника, формулы для вычисления площади различных видов треугольников в зависимости от известных исходных данных, калькулятор для нахождения площади онлайн и сводная таблица с формулами площадей треугольников.
Таблица с формулами площади треугольника (в конце страницы)
Скачать формулы площади треугольника в виде картинки или файла PDF (в конце страницы)
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)
Для всех треугольников
1
Площадь треугольника по основанию и высоте
Сторона a
Высота h
Основанием треугольника может быть выбрана любая из сторон треугольника.
2
Площадь треугольника по двум сторонам и углу между ними
Сторона a
Сторона b
Угол α° между сторонами a и b
Угол α между сторонами может быть любым: тупым, острым, прямым.
3
Площадь треугольника по радиусу вписанной окружности и трем сторонам
Сторона a
Сторона b
Сторона c
Радиус r вписанной окружности
4
Площадь треугольника по радиусу описанной окружности и трем сторонам
Сторона a
Сторона b
Сторона c
Радиус R описанной окружности
5
Площадь треугольника по формуле Герона
Полупериметр:
Сторона a
Сторона b
Сторона c
6
Площадь произвольного треугольника по стороне и двум прилежащим углам
Сторона a
Угол β°
Угол α°
Для равнобедренных треугольников
7
Площадь равнобедренного треугольника по боковым сторонам и основанию
Сторона a (a = b)
Сторона c
8
Площадь равнобедренного треугольника по боковым сторонам и углу между ними
Боковая сторона a (a = b)
Угол α° между боковыми сторонами
9
Площадь равнобедренного треугольника по боковой стороне, основанию и углу между ними
Боковая сторона a (a = b)
Основание треугольника c
Угол β° между основанием и стороной
10
Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами
Основание треугольника c
Угол α° между боковыми сторонами
Для равносторонних треугольников
11
Площадь равнобедренного треугольника по высоте и основанию
Основание треугольника c
Высота h
12
Площадь равностороннего треугольника по стороне
Сторона a (a = b = c)
13
Площадь равностороннего треугольника по высоте
Высота h
14
Площадь равностороннего треугольника по радиусу вписанной окружности
Радиус r вписанной окружности
15
Площадь равностороннего треугольника по радиусу описанной окружности
Радиус R описанной окружности
Для прямоугольных треугольников
16
Площадь прямоугольного треугольника по двум катетам
Катет a
Катет b
17
Площадь прямоугольного треугольника через гипотенузу и угол
Сторона c
Угол α
18
Площадь прямоугольного треугольника через катет и угол
Сторона b
Угол α
19
Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность
Отрезок d
Отрезок e
20
Площадь прямоугольного треугольника через гипотенузу и вписанную окружность
Сторона с
Радиус r
21
Площадь прямоугольного треугольника по формуле Герона
Полупериметр:
Сторона a
Сторона b
Сторона c
Для вычисления площади треугольника применяются различные формулы, в зависимости от известных исходных данных. Выше приведены формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные вычисления. Приведены общие формулы для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.
Выше приведены формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные вычисления. Приведены общие формулы для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.
Наш калькулятор для вычисления площади поможет вам вычислить площадь разных видов треугольников или проверить уже выполненные вычисления.
В зависимости от вида треугольника и его известных исходных данных, площадь треугольника можно вычислить по различным формулам.
Таблица с формулами площади треугольника
Определения
Площадь треугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя отрезками (сторонами), которые соединяют три точки (вершины), не лежащие на одной прямой.
Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника.
Отрезки называют сторонами треугольника, а точки – вершинами треугольника.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Скачать формулы площади треугольника в виде картинки
Считаем площадь неправильного 4-х угольника
Следующий калькулятор был создан по неоднократному запросу создать калькулятор, который бы смог считать площадь неправильного четырехугольника, в котором известны длины сторон.
Все мы понимаем, что данный четырехугольник может иметь любой вид (параллелограмма, квадрата, прямоугольника и так далее). Углы могут быть совершенно разные. По этому был создан уникальный калькулятор, который в реальном режиме прорисовывает четырехугольник и сразу считает его площадь, длины сторон нужно задать сразу вверху калькулятора, а потом нажать остановить на том четырехугольнике, площадь которого вы хотите посчитать.
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B. C.
C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
Как найти площадь неравностороннего прямоугольника
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Через диагонали и угол между ними
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
Через стороны и противолежащие углы
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
Площадь вписанного четырехугольника в окружность
Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
Площадь описанного четырехугольника около окружности через радиус
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн.
Площадь четырехугольника – это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.
Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.
В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.
Площадь четырехугольника по диагоналям и углу между ними
Площадь четырехугольника через стороны и углы между этими сторонами
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты
Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
Определения
Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться нашим «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:
Вычисляет площадь неправильного четырехугольника с известными длинами сторон
С завидным упорством некоторые пользователи Planetcalc оставляют запросы на создание калькулятора для расчета площади неправильного четырехугольника, для которого известны только длины сторон. Подумалось, что остановить их можно только написав вот такой шуточный калькулятор. (Нажмите кнопку «Остановить» для определения площади понравившегося Вам четырехугольника с заданными Вами сторонами).
с использованием Python OpenCV
Мы начали с изучения основ OpenCV, а затем выполнили некоторую базовую обработку изображений и манипуляции с изображениями, за которыми последовали сегментации изображений и многие другие операции с использованием OpenCV и языка Python. Здесь, в этом разделе, мы выполним простых методов обнаружения объектов с использованием сопоставления шаблонов. Мы найдем объект на изображении, а затем опишем его особенности. Элементы — это общие атрибуты изображения, такие как углы, края и т. Д.Мы также рассмотрим некоторые распространенные и популярные алгоритмы обнаружения объектов, такие как SIFT, SURF, FAST, BREIF и ORB .
Как было сказано в предыдущих руководствах, OpenCV — это библиотека Commuter Vision с открытым исходным кодом , которая имеет интерфейсы C ++, Python и Java и поддерживает Windows, Linux, Mac OS, iOS и Android. Таким образом, его можно легко установить в Raspberry Pi в среде Python и Linux. Raspberry Pi с OpenCV и подключенной камерой можно использовать для создания множества приложений для обработки изображений в реальном времени, таких как обнаружение лиц, блокировка лица, отслеживание объектов, обнаружение автомобильных номеров, система домашней безопасности и т. Д.
Raspberry Pi с OpenCV и подключенной камерой можно использовать для создания множества приложений для обработки изображений в реальном времени, таких как обнаружение лиц, блокировка лица, отслеживание объектов, обнаружение автомобильных номеров, система домашней безопасности и т. Д.
Обнаружение и распознавание объектов являются наиболее важным вариантом использования компьютерного зрения, они используются для таких мощных вещей, как
- Маркировка сцен
- Робот-навигация
- Беспилотные автомобили
- Распознавание тела (Microsoft Kinect)
- Выявление болезней и рака
- Распознавание лиц
- Распознавание рукописного ввода
- Обозначение объектов на космических снимках
Обнаружение объектов VS Распознавание
Распознавание объектов — это второй уровень обнаружения объектов, при котором компьютер может распознавать объект из множества объектов на изображении и может идентифицировать его.
Теперь мы выполним некоторые функции обработки изображений, чтобы найти объект на изображении.
Поиск объекта по изображению
Здесь мы будем использовать сопоставление шаблонов для поиска символа / объекта на изображении, используйте функцию OpenCV cv2.matchTemplate () для поиска этого объекта
импортное CV2 импорт numpy как np
Загрузить исходное изображение и преобразовать его в серый
изображение = cv2.imread ('WaldoBeach.jpg')
cv2.imshow ('люди', изображение)
cv2.waitKey (0)
серый = cv2.cvtColor (изображение, cv2.COLOR_BGR2GRAY) Загрузить изображение шаблона
template = cv2.imread ('waldo.jpg', 0)
# результат сопоставления шаблона объекта поверх изображения
результат = cv2. matchTemplate (серый, шаблон, cv2.TM_CCOEFF)
sin_val, max_val, min_loc, max_loc = cv2.minMaxLoc (результат)
matchTemplate (серый, шаблон, cv2.TM_CCOEFF)
sin_val, max_val, min_loc, max_loc = cv2.minMaxLoc (результат) Создать ограничивающую рамку
top_left = max_loc
# увеличение размера ограничивающего прямоугольника на 50 пикселей
bottom_right = (top_left [0] + 50, top_left [1] +50)
cv2.прямоугольник (image, top_left, bottom_right, (0,255,0), 5)
cv2.imshow ('объект найден', изображение)
cv2.waitKey (0)
cv2.destroyAllWindows () В cv2.matchTemplate (серый, шаблон, cv2.TM_CCOEFF) введите полутоновое изображение, чтобы найти объект и шаблон. Затем примените метод сопоставления шаблонов для поиска объектов на изображении, здесь cv2.Используется TM_CCOEFF .
Вся функция возвращает массив, который вводится в результат, который является результатом процедуры сопоставления шаблонов.
Затем мы используем cv2.minMaxLoc (result) , который дает координаты или ограничивающую рамку, в которой объект был найден на изображении, и когда мы получим эти координаты, нарисуем прямоугольник над ним и немного растянем размеры объекта. box, чтобы объект мог легко поместиться внутри прямоугольника.
Существует множество методов сопоставления шаблонов, и в данном случае мы используем cv2.TM_CCOEFF , что означает коэффициент корреляции.
cv2.matchTemplate берет «скользящее окно» объекта и перемещает его по изображению слева направо и сверху вниз, по одному пикселю за раз. Затем для каждого местоположения мы вычисляем коэффициент корреляции, чтобы определить, насколько «хорошее» или «плохое» совпадение.
Области с достаточно высокой корреляцией можно рассматривать как совпадения, оттуда все, что нам нужно, это вызвать cv2.minMaxLoc , чтобы найти хорошие совпадения в сопоставлении с шаблоном.
Характеристика Описание Теория
При сопоставлении шаблона мы перемещаем изображение шаблона по исходному изображению, пока не будет найдено совпадение. Но это не лучший метод распознавания объектов, так как он имеет серьезные ограничения. Этот метод не очень устойчивый.
Но это не лучший метод распознавания объектов, так как он имеет серьезные ограничения. Этот метод не очень устойчивый.
Следующие факторы делают сопоставление с шаблоном плохим выбором для обнаружения объектов.
- Вращение делает этот метод неэффективным.
- Размер (известный как масштабирование) также влияет на это.
- Фотометрические изменения (например, яркость, контраст, оттенок и т. Д.)
- Искажение изменения точки обзора формы (Affine).
Единственное решение этой проблемы — функций изображения
Характеристики изображения — это интересные области изображения, которые в некоторой степени уникальны для этого конкретного изображения. Их также называют ключевых точек или процентных точек .
Небо — неинтересная особенность, в то время как определенные ключевые точки (отмеченные красными кружками) могут использоваться для обнаружения вышеуказанного изображения (интересные особенности).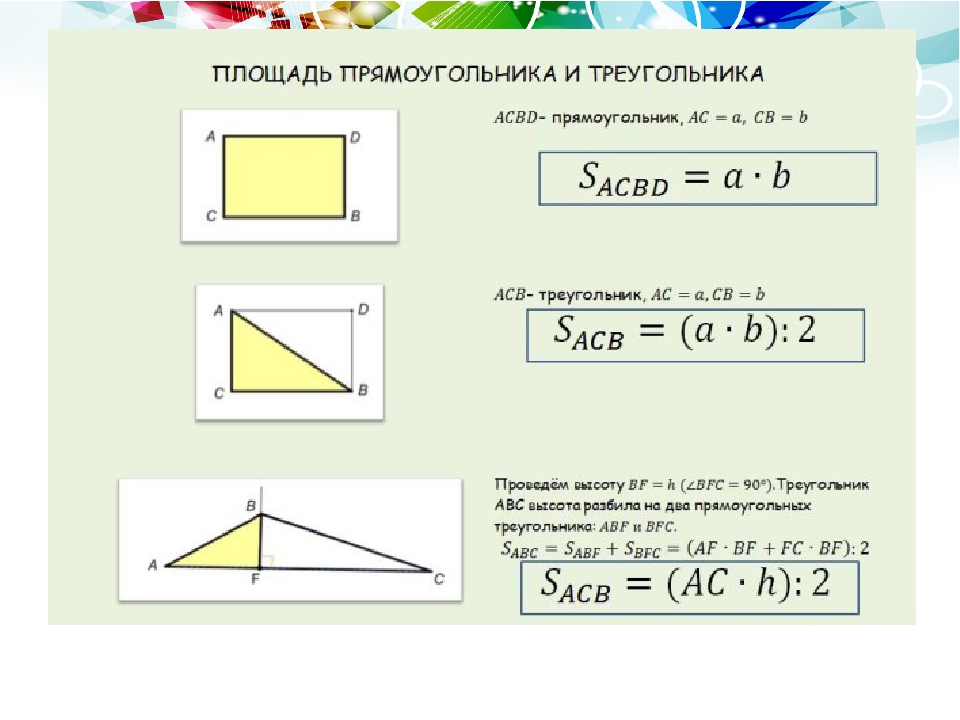 Изображение, показанное выше, ясно показывает разницу между интересной функцией и неинтересной функцией.
Изображение, показанное выше, ясно показывает разницу между интересной функцией и неинтересной функцией.
Важность обнаружения признаков
Функции важны, поскольку их можно использовать для анализа, описания и сопоставления изображений. Они широко используются в:
- Выравнивание изображения — например, сшивание панорамы (поиск соответствующих совпадений, чтобы мы могли сшить изображения)
- 3D реконструкция
- Робот-навигация
- Распознавание объекта
- Отслеживание движения
- И многое другое!
Что определяет точки интереса?
Интересные области несут много четкой информации и уникальной информации о местности.Как правило, это области с сильным изменением интенсивности, углы или края и многое другое. Но всегда будьте осторожны, поскольку шум может показаться «информативным», когда это не так! Так что попробуйте размыть, чтобы уменьшить шум.
Характеристики хороших или интересных характеристик
Repeatable — Их можно найти на нескольких изображениях одной и той же сцены.
Отличительный — Каждая функция в некоторой степени уникальна и отличается от других функций той же сцены.
Компактность / эффективность — На изображении заметно меньше элементов, чем пикселей.
Местоположение — Элемент занимает небольшую область изображения и устойчив к беспорядку и засорению.
Углы как элементы
Углы идентифицируются, когда смещение окна в любом направлении над этой точкой дает большое изменение интенсивности.
Уголки — не лучший вариант для идентификации изображений, но да, у них определенно есть хорошие варианты их использования, которые делают их удобными в использовании.
Итак, чтобы определить углы на вашем изображении, представьте зеленое окно, на которое мы смотрим, а черное — это изображение, в котором мы хотим найти углы, и теперь, когда мы перемещаем окно только внутри черного ящика, мы видим, что в нем нет изменений. интенсивности и, следовательно, изображение плоское, т.е. углы не определены.
интенсивности и, следовательно, изображение плоское, т.е. углы не определены.
Теперь, когда мы перемещаем окно в одном направлении, мы видим, что есть изменение интенсивности только в одном направлении, следовательно, это край, а не угол.
Когда мы перемещаем окно в угол, и независимо от того, в каком направлении мы перемещаем окно, теперь происходит изменение интенсивности, и это определяется как угол.
Итак, давайте определим угол с помощью алгоритма Harris Corner Detection, разработанного в 1998 году для обнаружения углов и работающего достаточно хорошо.
Следующая функция OpenCV используется для обнаружения углов.
cv2.cornerHarris (входное изображение, размер блока, ksize, k)
Входное изображение — Должно быть в оттенках серого и типом float32.
blockSize — Размер окрестности, учитываемой для обнаружения угла
ksize — Используемый апертурный параметр производной Собеля.
k — Свободный параметр детектора Харриса в уравнении
Выход — массив угловых точек (x, y)
Также важно отметить, что алгоритм обнаружения углов Харриса требует типа данных массива с плавающей запятой 32 изображения , т.е. изображение должно быть серым изображением типа с плавающей запятой 32.
импортное CV2 импорт numpy как np
Загрузить изображение, затем оттенки серого
изображение = cv2.imread ('chess.jpg')
серый = cv2.cvtColor (изображение, cv2.COLOR_BGR2GRAY) Функция cornerHarris требует, чтобы тип данных массива был float32
серый = np.float32 (серый) harris_corners = cv2.cornerHarris (серый, 3, 3, 0,05)
Для увеличения используем расширение угловых точек
ядро = np.ones ((7,7), np.uint8) harris_corners = cv2.расширять (harris_corners, ядро, итераций = 2)
Порог оптимального значения, он может варьироваться в зависимости от изображения
изображение [harris_corners> 0,025 * harris_corners.max ()] = [255, 127, 127]
cv2.imshow ('Харрис Корнерс', изображение)
cv2.waitKey (0)
cv2.destroyAllWindows () Corner Harris возвращает расположение углов, поэтому для визуализации этих крошечных мест мы используем расширение, чтобы добавить пиксели к краям углов.Итак, чтобы увеличить угол, мы дважды выполняем растяжение. Затем мы снова задаем пороговые значения, чтобы изменить цвета углов.
Следующая функция используется для того же с указанными ниже параметрами
cv2.goodFeaturesToTrack (входное изображение, maxCorners, qualityLevel, minDistance)
- Входное изображение — 8-битное или 32-битное с плавающей запятой, одноканальное изображение.

- maxCorners — Максимальное количество возвращаемых углов.Если количество углов больше, чем общее количество фактически обнаруженных углов, то возвращается самый сильный из них.
- qualityLevel — Параметр, характеризующий минимально допустимое качество углов изображения. Значение параметра умножается на лучший показатель качества углов (наименьшее собственное значение). Углы с показателем качества меньше продукта отбраковываются. Например, если для лучшего угла показатель качества = 1500, а уровень качества = 0.01, то отбраковываются все углы с качеством менее 15.
- minDistance — Минимально возможное евклидово расстояние между возвращенными углами.
импортное CV2
импортировать numpy как np
img = cv2.imread ('chess.jpg')
серый = cv2.cvtColor (img, cv2.COLOR_BGR2GRAY) Уточняем верхние 50 углов
углов = cv2.goodFeaturesToTrack (серый, 100, 0.01, 15) для угла в углах: x, y = угол [0] х = целое (х) y = int (y) cv2. rectangle (img, (x-10, y-10), (x + 10, y + 10), (0,255,0), 2) cv2.imshow ("Углы найдены", img) cv2.waitKey () cv2.destroyAllWindows ()
Он также возвращает массив местоположения углов, как и предыдущий метод, поэтому мы перебираем каждую из угловых позиций и наносим на нее прямоугольник.
Проблемы с углами как особенности
Согласование углов на изображениях допустимо, или обнаружение углов не имеет проблем с обнаружением изображения, когда изображение
• Повернутое
• Сдвинутое (т.е. сдвиг изображения)
• Небольшие фотометрические изменения, например яркость
или аффинная интенсивность
Однако он не переносит из:
• Значительные изменения интенсивности или фотометрические изменения
)
• Масштабирование (т. е.е. увеличение или уменьшение)
е.е. увеличение или уменьшение)
Алгоритмы SIFT, SURF, FAST, BRIEF и ORB
Масштабно-инвариантное преобразование признаков (SIFT)
Угловые детекторы, такие как алгоритм определения углов Харриса , инвариантны к повороту, что означает, что даже если изображение повернуто, мы все равно можем получить те же углы. Это также очевидно, поскольку углы остаются углами и на повернутом изображении. Но когда мы масштабируем изображение, угол может быть не таким, как показано на изображении выше.
SIFT используется для обнаружения интересных ключевых точек в изображении с использованием разностного метода Гаусса, это области изображения, где отклонения превышают определенный порог и лучше, чем дескриптор края.
Затем мы создаем векторный дескриптор для этих интересных областей. Масштабная инвариантность достигается с помощью следующего процесса:
i.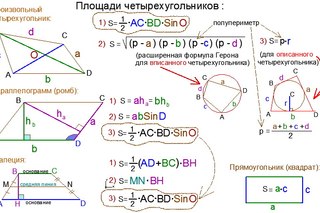 Интересные точки сканируются на в нескольких разных масштабах.
Интересные точки сканируются на в нескольких разных масштабах.
ii. Затем с помощью дескриптора вектора выбирается и кодируется масштаб, при котором мы удовлетворяем конкретному критерию стабильности .Таким образом, независимо от начального размера, обнаруживается более стабильный масштаб, который позволяет нам быть инвариантным к масштабу.
Инвариантность вращения достигается путем получения Назначение ориентации ключевой точки с использованием величин градиента изображения. Как только мы узнаем 2D-направление, мы можем нормализовать это направление.
Полную статью о SIFT можно прочитать здесь:
http://www.cs.ubc.ca/~lowe/papers/ijcv04.pdf.
И вы также можете найти руководство по официальной ссылке OpenCV.
Ускоренные надежные функции (SURF)
SURF — это ускоренная версия SIFT, так как SIFT требует больших вычислительных ресурсов.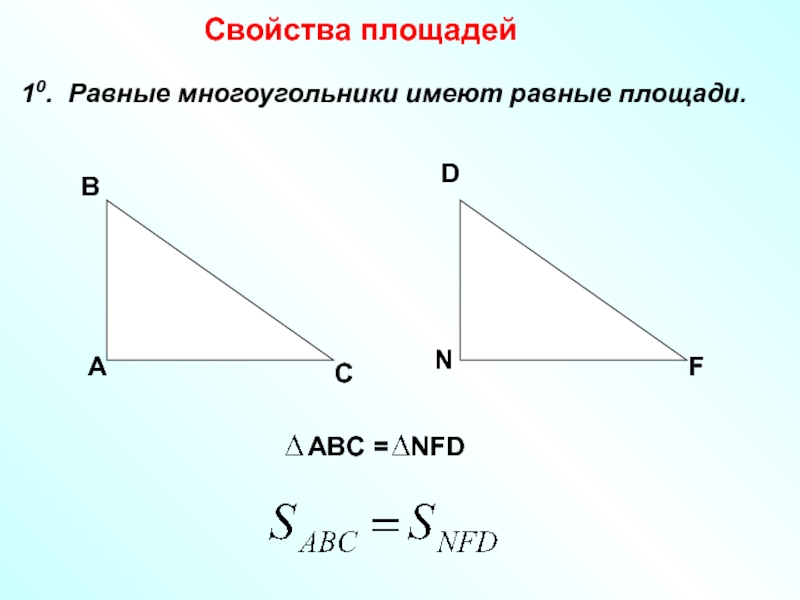
SURF был разработан для повышения быстродействия масштабно-инвариантного детектора признаков. Вместо использования подхода различия гаусса, SURF использует приближение матрицы Гессе для обнаружения интересных точек и использует сумму откликов вейвлета Хаара для назначения ориентации.
Полную статью о SIFT можно прочитать здесь: http://www.vision.ee.ethz.ch/~surf/eccv06.pdf
Альтернативы SIFT и SURF
Поскольку SIFT и SURF запатентованы, они не доступны для коммерческого использования в свободном доступе, однако есть альтернативы этим алгоритмам, которые кратко описаны здесь
Функции ускоренного тестирования сегмента (FAST)
• Только обнаружение ключевой точки (без дескриптора, мы можем использовать SIFT или SURF для вычисления)
• Используется в приложениях реального времени
Здесь вы можете найти статьи по FAST
https: // www.edwardrosten.com/work/rosten_2006_machine. pdf
pdf
Двоичные устойчивые независимые элементарные функции (КРАТКОЕ ОПИСАНИЕ)
• Дескрипторы компьютеров быстро (вместо использования SIFT или SURF)
• Это довольно быстро.
Здесь вы можете найти статью о BRIEF
http://cvlabwww.epfl.ch/~lepetit/papers/calonder_pami11.pdf
Ориентированный БЫСТРЫЙ и повернутый КРАТКИЙ ОБЗОР (ORB)
- Разработано на основе OpenCV Labs (не запатентовано, поэтому можно использовать бесплатно!)
- Сочетает в себе как быстрое, так и краткое
Здесь вы можете найти статью по ORB
http: // www.willowgarage.com/sites/default/files/orb_final.pdf
Использование SIFT, SURF, FAST, BRIEF и ORB в OpenCV
Реализация функции обнаружения
Алгоритмы SIFT и SURF запатентованы их соответствующими создателями, и, хотя они бесплатны для использования в академических и исследовательских целях, технически вы должны получить лицензию / разрешение от создателей, если вы используете их в коммерческих целях (т. е.е. для получения прибыли) приложение.
е.е. для получения прибыли) приложение.
Ниже мы объясняем примеры программирования всех упомянутых выше алгоритмов.
SIFT
импортное CV2
импортировать numpy как np
image = cv2.imread ('paris.jpg')
серый = cv2.cvtColor (изображение, cv2.COLOR_BGR2GRAY)
Создать объект "Детектор признаков SIFT"
sift = cv2.xfeatures2d.SIFT_create ()
# Обнаружить ключевые точки
ключевых точки = просеять.обнаружить (серый, нет)
print («Количество обнаруженных ключевых точек:», len (ключевые точки)) Нарисуйте насыщенные ключевые точки на входном изображении
image = cv2.drawKeypoints (изображение, ключевые точки, Нет, флаги = cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS) cv2.imshow ('Feature Method - SIFT', image) cv2.waitKey (0) cv2.destroyAllWindows ()
Вывод консоли:
Количество обнаруженных ключевых точек: 1893
Здесь ключевыми точками являются координаты (X, Y), извлеченные с помощью детектора просеивания и нарисованные поверх изображения с помощью функции cv2 draw keypoint.
SURF
импортное CV2
импортировать numpy как np
image = cv2.imread ('paris.jpg')
серый = cv2.cvtColor (изображение, cv2.COLOR_BGR2GRAY) Создайте объект SURF Feature Detector, здесь мы устанавливаем порог гессиана на 500
# Детектор сохраняет только те элементы, гессиан которых больше, чем порог гессиана.
# вы можете увеличить значение порога гессиана, чтобы уменьшить ключевые точки
серф = cv2.xfeatures2d.SURF_create (500) ключевых точек, дескрипторы = surf.detectAndCompute (серый, нет) print («Количество обнаруженных ключевых точек:», len (ключевые точки))
Нарисуйте насыщенные ключевые точки на входном изображении
image = cv2.drawKeypoints (изображение, ключевые точки, Нет, флаги = cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
cv2.imshow ('Feature Method - SURF', image)
cv2.waitKey ()
cv2.destroyAllWindows () Вывод консоли:
Количество обнаруженных ключевых точек: 1548
БЫСТРО
импортное CV2
импортировать numpy как np
изображение = cv2.imread ('paris.jpg')
серый = cv2.cvtColor (изображение, cv2.COLOR_BGR2GRAY) Создать объект FAST Detector
быстро = cv2.FastFeatureDetector_create () # Получить ключевые точки, по умолчанию не максимальное подавление включено # для выключения set fast.setBool ('nonmaxSuppression', False) ключевых точек = fast.detect (серый, нет) print («Количество обнаруженных ключевых точек:», len (ключевые точки))
Нарисовать сложные ключевые точки на входном изображении
изображение = cv2.drawKeypoints (изображение, ключевые точки, None, flags = cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
cv2.imshow ('Feature Method - FAST', image)
cv2.waitKey ()
cv2.destroyAllWindows () Вывод консоли:
Количество обнаруженных ключевых точек: 8960
КРАТКАЯ
импортное CV2 импортировать numpy как np image = cv2.imread ('paris.jpg ') серый = cv2.cvtColor (изображение, cv2.COLOR_BGR2GRAY)
Создать объект детектора FAST
short = cv2.xfeatures2d.BriefDescriptorExtractor_create ()
Создать объект экстрактора BRIEF
#brief = cv2.DescriptorExtractor_create ("BRIEF")
# Определить ключевые точки
ключевых точек = fast.detect (серый, нет) Получите дескрипторы и новые конечные ключевые точки с помощью BRIEF
ключевых точки, дескрипторы = краткие.вычислить (серый, ключевые точки) print («Количество обнаруженных ключевых точек:», len (ключевые точки))
Нарисовать сложные ключевые точки на входном изображении
image = cv2.drawKeypoints (изображение, ключевые точки, None, flags = cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS) cv2.imshow ('Feature Method - BRIEF', image) cv2.waitKey () cv2.destroyAllWindows ()
Вывод консоли:
Количество обнаруженных ключевых точек: 8735
ORB
импортное CV2
импортировать numpy как np
изображение = cv2.imread ('paris.jpg')
серый = cv2.cvtColor (изображение, cv2.COLOR_BGR2GRAY) Создайте объект ORB, мы можем указать количество желаемых ключевых точек
orb = cv2.ORB_create () # Определить ключевые точки ключевых точек = orb.detect (серый, Нет)
Получить дескрипторы
ключевых точек, дескрипторы = orb.compute (серый, ключевые точки) print («Количество обнаруженных ключевых точек:», len (ключевые точки))
Нарисовать сложные ключевые точки на входном изображении
изображение = cv2.drawKeypoints (изображение, ключевые точки, None, flags = cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
cv2.imshow ('Feature Method - ORB', изображение)
cv2.waitKey ()
cv2.destroyAllWindows () Вывод консоли:
Количество обнаруженных ключевых точек: 500
Мы можем указать количество ключевых точек с максимальным пределом 5000, однако значение по умолчанию — 500, то есть ORB автоматически обнаружит 500 лучших ключевых точек, если не указано для какого-либо значения ключевых точек.
Таким образом, обнаружение объектов происходит в OpenCV. Те же программы можно запускать в Raspberry Pi с установленным OpenCV и использовать их в качестве портативных устройств, например смартфонов с Google Lens.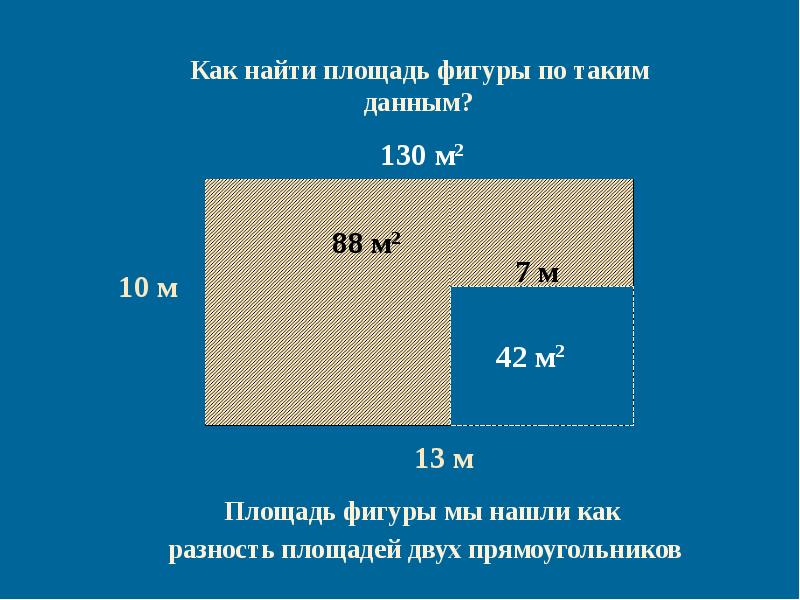
Эта статья ссылается на Master Computer Vision ™ OpenCV4 в Python с курсом глубокого обучения по Udemy, созданным Радживом Ратаном, подпишитесь на нее, чтобы узнать больше о компьютерном зрении и Python.
Расстояние между
Этот инструмент можно использовать для определения расстояния между двумя именованными точками на карте.Вы можете решить, какие две точки измерять, а затем узнать расстояние между ними по прямой и расстояние при движении. Введите названия мест ниже и нажмите кнопку «Показать».
Как использовать
Просто введите названия двух мест в текстовых полях и нажмите кнопку «Показать»!
Наилучший формат для ввода местоположения — [Город, Страна], то есть [Город (запятая) (пробел) Страна]. Вы также можете печатать прямо в основных местах, таких как «США», «Токио», «Лондон» и т. Д.Также можно использовать почтовые индексы и адреса.
Когда вы нажимаете кнопку поиска, будет произведен поиск, чтобы найти то место, о котором вы говорите.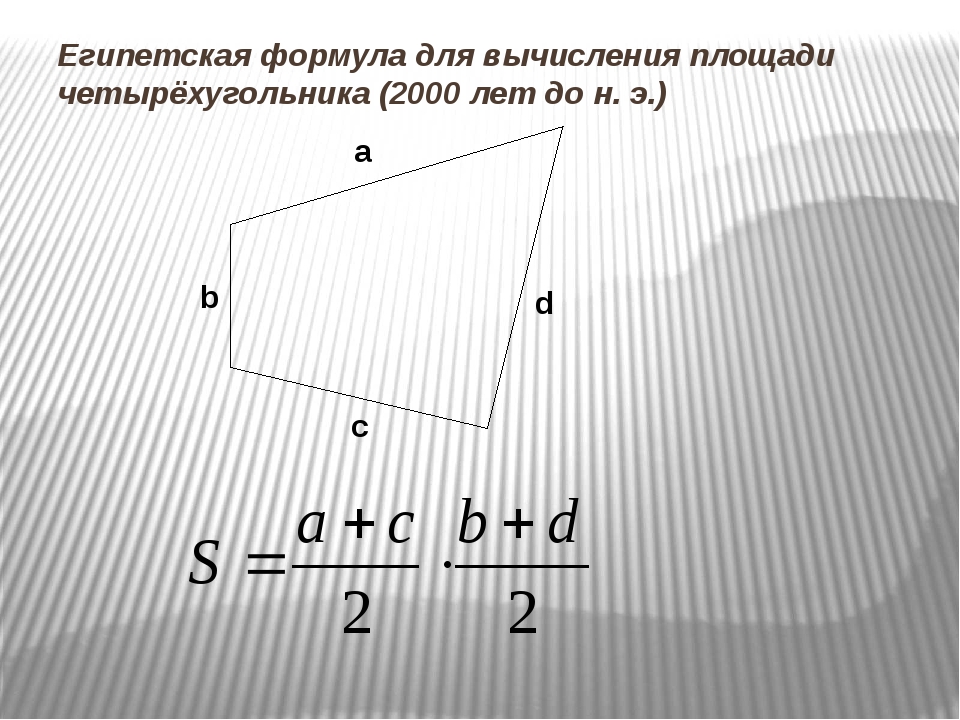 Во-первых, производится поиск по внутреннему списку общих мест. Если совпадений не найдено, поиск будет выполнен с использованием функции GlocalSearch API Карт Google. Если и это не дает результатов, вас попросят указать местоположение точки, щелкнув карту. Это позволяет вам увидеть расстояние между двумя точками, а также ввести местоположение во внутреннюю базу данных, чтобы в следующий раз, когда посетитель будет искать это местоположение, оно будет найдено.
Во-первых, производится поиск по внутреннему списку общих мест. Если совпадений не найдено, поиск будет выполнен с использованием функции GlocalSearch API Карт Google. Если и это не дает результатов, вас попросят указать местоположение точки, щелкнув карту. Это позволяет вам увидеть расстояние между двумя точками, а также ввести местоположение во внутреннюю базу данных, чтобы в следующий раз, когда посетитель будет искать это местоположение, оно будет найдено.
Как только результат будет возвращен, вы можете скопировать URL-адрес, чтобы использовать его в качестве постоянной ссылки обратно на результат для вашей собственной ссылки или для передачи другим людям.
Примечание : для почтовых индексов используйте расстояние между почтовыми индексами, для почтовых индексов Великобритании используйте инструмент расстояния для почтовых индексов Великобритании. Кроме того, чтобы найти расстояние между точками, которые не названы, вы можете использовать инструмент «Измерить расстояние».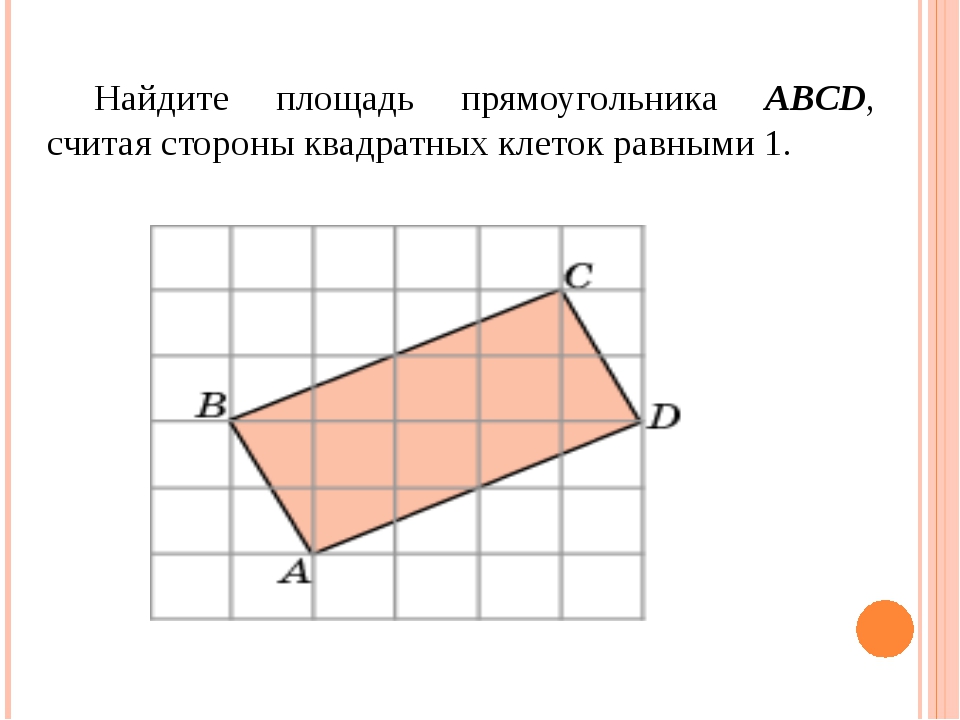
О том, как далеко между
Этот инструмент можно использовать для определения расстояния между странами, городами или поселками.
Выводятся два расстояния:
- Как летит ворона — Прямое расстояние между точками
- Расстояние наземным транспортом (если возможно) — оценка расстояния при движении по дороге и по морю.
Расстояния можно вывести в следующих единицах:
Результатом является измерение расстояния, а также карта, которая показывает эти два местоположения и путь между ними по прямой, а также маршрут наземным транспортом.
Вы можете использовать элементы управления на карте, чтобы:
- Переместить карту
- Увеличить карту
- Переключение между режимами просмотра карты и спутников
Некоторые примеры расстояний
Некоторые расстояния между городами, которые можно найти с помощью системы.Щелкните по одному из них, чтобы увидеть его, или введите свое собственное место выше в текстовые поля.
- Как далеко от Сиднея, Австралия, до Лондона, Англия
- Как далеко от Лондона, Великобритания, до Берлина, Германия
- Как далеко от Бристоля, Англия, до Шанхая, Китай
- Как далеко от Бразилия, Южная Америка и Лестер, Англия
- Как далеко от Флоренции, Италия, до Глазго, Шотландия
Известные проблемы
- Красная линия не пересекает международную линию перемены дат
- Автоматический зум не работает, когда кратчайшее расстояние пересекает международную линию перемены дат
- Разрешить запрашивать точки на удаление из базы данных, чтобы информация оставалась аккуратной
Если вы заметите что-то, что требует решения, обратитесь в Free Map Tools.
История версий
- 15 октября 2018: Исправлена ошибка, неверное расстояние, когда маршрут пересекал IDL
- 30 сентября 2018: Исправление ошибки, некорректное поведение после расчета 2-го, 3-го и т. Д. Маршрута
- 28 сентября 2018: Исправлена ошибка, при вычислении 2-го расстояния возникала ошибка
- 21 сентября 2018: исправлена проблема с форматом времени в пути
- 19 сентября 2018 г .
 : переключено на листовки карт
: переключено на листовки карт - 14 ноября 2016 г .: теперь выводится продолжительность поездки, если применимо.
- 28 июня 2016 г .: вывод URL теперь содержит информацию о единицах измерения (KM)
- 22 июня 2016 г .: настройка км / миль теперь будет сохранять и запоминать свое состояние между сеансами
- 28 мая 2015 г .: Теперь использует места Google.Автозаполнение
- 15 марта 2015: новая возможность объезжать автомагистрали / автомагистрали
- 27 января 2015: добавлена кнопка полноэкранного режима
- 8 января 2014 г .: Устранена незначительная проблема. Когда маршруты проезда не найдены, в поле отображается надпись «Н / Д». Ранее он не обновлялся и иногда сохранял значение расстояния предыдущего поиска.
- , 7 января 2014 г .: Решена незначительная проблема, из-за которой маршруты проезда из старого измерения все еще отображались, когда выполнялся другой поиск.
- 13 ноября 2013 г .: Реализован API Карт Google версии 3
- 7 марта 2010: Добавлен новый вид транспорта.
 .. Пассажирский самолет
.. Пассажирский самолет - 2 декабря 2009 г .: Теперь предлагаемые города и страны отображаются намного быстрее. Также показывает самые популярные места вверху списка
- 20 января 2008 г .: Улучшено автоматическое масштабирование для получения более точных результатов
- 15 декабря 2007: добавлена опция сохранения данных
- 29 ноября 2007: Добавлена опция измерения наземного транспорта
- , 4 ноября 2007 г .: динамический URL для сохранения расстояния между X и Y
- 21 октября 2007: Добавлен поиск GlocalSearch для автоматического поиска других мест
- , 18 июля 2007 г. Исправлены раскрывающиеся списки, поэтому они перекрывают все содержимое ниже .
- , 1 июля 2007 г .: Работа над разрешением пользователям добавлять новые местоположения, если они не находятся в системе.
- 30 июня 2007 г .: Страница создана с использованием базовой функциональности
Соответствующие ссылки
Leaflet — JavaScript-библиотека для интерактивных карт
Площадь прямоугольника — определение, формула и задачи
Любая замкнутая форма, состоящая как минимум из трехстрочных сегментов, называется многоугольником. Есть много различных типов многоугольников, некоторые из которых являются треугольниками, четырехугольниками, пятиугольниками, шестиугольниками и т. Д. Многоугольники классифицируются по количеству ребер, которые у них есть. Кромки также называются сторонами, и они представляют собой не что иное, как отрезки линий, составляющие многоугольники. Точки пересечения отрезков называются вершинами. У многоугольника одинаковое количество ребер и вершин.
Есть много различных типов многоугольников, некоторые из которых являются треугольниками, четырехугольниками, пятиугольниками, шестиугольниками и т. Д. Многоугольники классифицируются по количеству ребер, которые у них есть. Кромки также называются сторонами, и они представляют собой не что иное, как отрезки линий, составляющие многоугольники. Точки пересечения отрезков называются вершинами. У многоугольника одинаковое количество ребер и вершин.
Полигоны классифицируются по количеству ребер или вершин, которые у них есть. Многоугольник с четырьмя сторонами называется четырехугольником или четырехугольником.Четырехугольники можно дополнительно разделить на вогнутые четырехугольники, выпуклые четырехугольники и прямоугольные четырехугольники на основе углов, которые они содержат. Если все четыре стороны четырехугольника равны 90 °, они являются прямоугольными четырехугольниками. Их еще называют равносторонними четырехугольниками, так как все их углы равны. Два типа равносторонних четырехугольников — это квадраты и прямоугольники. В квадрате все четыре стороны четырехугольника равны. В прямоугольнике равны только противоположные стороны четырехугольника.
В квадрате все четыре стороны четырехугольника равны. В прямоугольнике равны только противоположные стороны четырехугольника.
Поскольку противоположные стороны квадрата равны, квадрат также можно рассматривать как прямоугольник. Прямоугольник также является параллелограммом, что означает, что противоположные стороны прямоугольника идеально параллельны друг другу. Также можно сказать, что прямоугольник, все четыре стороны которого равны друг другу, есть квадрат.
Площадь прямоугольника:
Площадь любого многоугольника — это размер пространства, которое он занимает или охватывает. Это количество квадратных единиц внутри многоугольника.Площадь — это двухмерное свойство, что означает, что она содержит длину и ширину. Площадь обычно измеряется в квадратных метрах, квадратных футах или квадратных дюймах. Площадь более крупных форм, таких как поля или города, измеряется в квадратных километрах, гектарах или акрах.
Чтобы найти площадь прямоугольника, нам просто нужно умножить его длину на ширину.
Площадь — это просто ширина прямоугольника, умноженная на высоту.
Формула для вычисления площади прямоугольника имеет следующий вид:
Площадь = ш × в
Например, если прямоугольник имеет ширину 8 м и высоту 3 м,
Площадь прямоугольника равна Площадь = ш × h
Площадь = 8 × 3
Площадь = 24 м 2
В квадрате, поскольку все четыре стороны равны, Area = w × h становится
Area = h × h, Area = h 2 .
Следовательно, площадь квадрата равна квадрату его сторон.
Задачи, связанные с площадью прямоугольника:
1) Найдите площадь прямоугольника высотой 20 см и шириной 4 см.
Решение: задано, высота = 20 см и ширина = 4 см
Площадь прямоугольника = ширина × высота
Площадь прямоугольника = 20 × 4
Следовательно, площадь прямоугольника = 80 см 2 .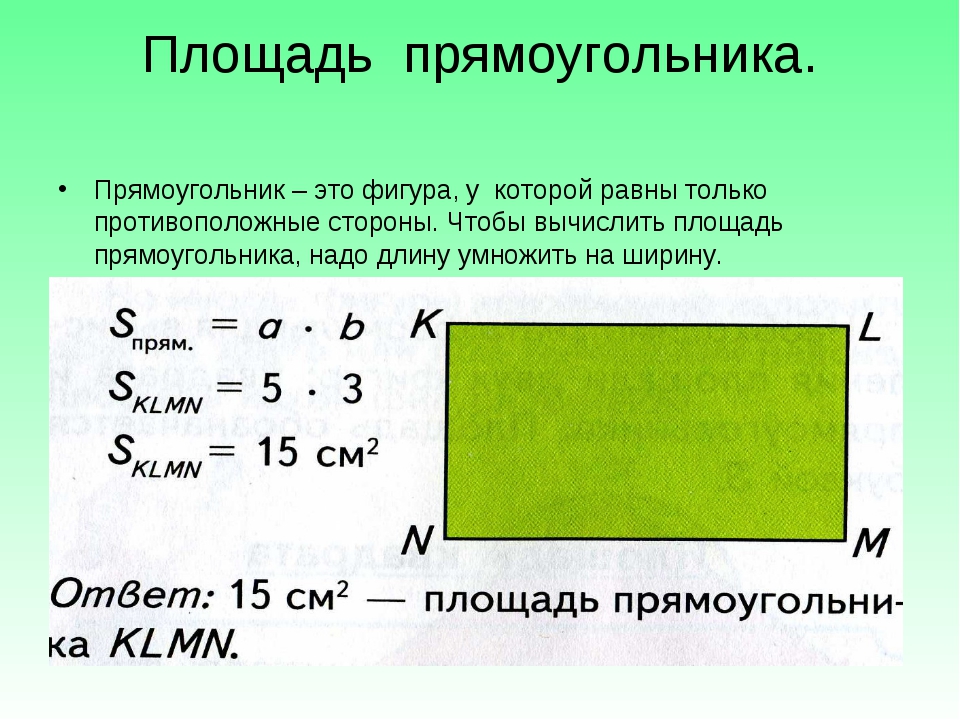
2) Доска прямоугольной формы имеет ширину 120 мм и высоту 89 мм.Найдите площадь этой доски.
Решение: задано, высота = 89 мм = 8,9 см и ширина = 120 мм = 12 см
Площадь прямоугольника = ширина × высота
Площадь прямоугольника = 12 × 8,9
Следовательно, площадь прямоугольника прямоугольник = 106,8 см 2 .
3) Высота прямоугольного экрана составляет 20 см. Его площадь составляет 240 см 2 . Найдите ширину данного экрана.
Решение: задано, высота = 20 см, площадь = 240 см 2 .
Площадь прямоугольника = Ш × В
Следовательно, Ширина = Площадь / длина
Ширина = 240/20
Ширина = 120 см
4) Высота и ширина прямоугольной стены составляют 80 м и 60 м соответственно. Если маляр взимает 3 фунта стерлингов за м 2 2 за покраску стены, сколько будет стоить покраска всей стены?
Решение: задано, высота = 80 м и ширина = 60 м
Площадь прямоугольника = ш × в
Площадь прямоугольника = 80 × 60
Площадь прямоугольника = 4800 м 2
При стоимость 3 ₹ за м 2 , стоимость покраски 4800 м 2 4800 × 3 = 14 400 ₹
5) Пол длиной и шириной 60 м и 40 м, соответственно, необходимо покрыть прямоугольным плитки.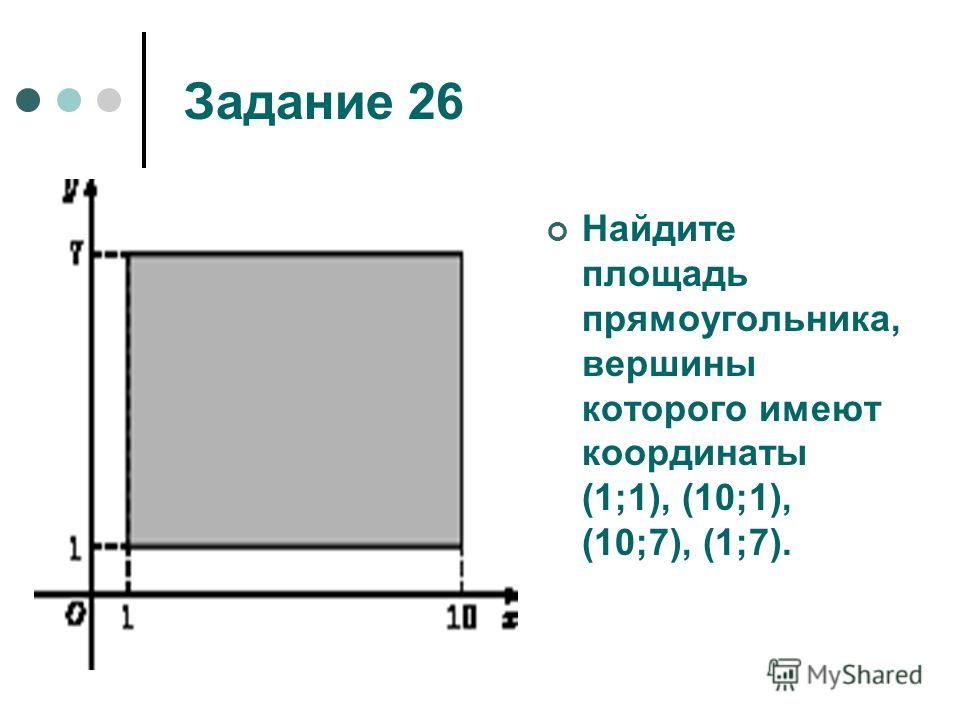 Размер выбранной напольной плитки — 1 м × 2 м. Найдите общее количество плиток, необходимое для полного покрытия комнаты.
Размер выбранной напольной плитки — 1 м × 2 м. Найдите общее количество плиток, необходимое для полного покрытия комнаты.
Решение: задано, длина = 60 м и ширина = 40 м
Площадь прямоугольника = ш × в
Площадь прямоугольника = 60 × 40
Площадь прямоугольника = 2400 м 2
длина одной плитки = 1 м
Ширина одной плитки = 2 м
Площадь = ш × в
Площадь одной плитки = 1 × 2
Площадь одной плитки = 2 м 2
Количество плиток Необходимые для покрытия пола можно посчитать по
Площадь пола / Площадь плитки
2400/2 = 1200 плиток.
6) Квадратный кусок картона площадью 36 см 2 вырезается из прямоугольного куска картона. Найдите
(a) Длина квадрата
(b) Если картон можно разрезать на три таких квадрата, найдите длину, ширину и площадь этого прямоугольного куска картона.
 Этот параметр меняется от 1 до n;
Этот параметр меняется от 1 до n;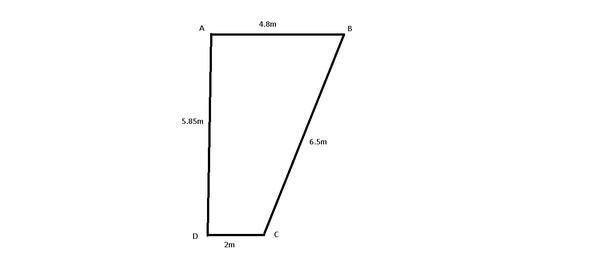 Это бесплатно.
Это бесплатно.
 matchTemplate (серый, шаблон, cv2.TM_CCOEFF)
sin_val, max_val, min_loc, max_loc = cv2.minMaxLoc (результат)
matchTemplate (серый, шаблон, cv2.TM_CCOEFF)
sin_val, max_val, min_loc, max_loc = cv2.minMaxLoc (результат)  ones ((7,7), np.uint8)
harris_corners = cv2.расширять (harris_corners, ядро, итераций = 2)
ones ((7,7), np.uint8)
harris_corners = cv2.расширять (harris_corners, ядро, итераций = 2) 
 goodFeaturesToTrack (серый, 100, 0.01, 15)
для угла в углах:
x, y = угол [0]
х = целое (х)
y = int (y)
cv2. rectangle (img, (x-10, y-10), (x + 10, y + 10), (0,255,0), 2)
cv2.imshow ("Углы найдены", img)
cv2.waitKey ()
cv2.destroyAllWindows ()
goodFeaturesToTrack (серый, 100, 0.01, 15)
для угла в углах:
x, y = угол [0]
х = целое (х)
y = int (y)
cv2. rectangle (img, (x-10, y-10), (x + 10, y + 10), (0,255,0), 2)
cv2.imshow ("Углы найдены", img)
cv2.waitKey ()
cv2.destroyAllWindows ()  imshow ('Feature Method - SIFT', image)
cv2.waitKey (0)
cv2.destroyAllWindows ()
imshow ('Feature Method - SIFT', image)
cv2.waitKey (0)
cv2.destroyAllWindows ()  xfeatures2d.SURF_create (500)
ключевых точек, дескрипторы = surf.detectAndCompute (серый, нет)
print («Количество обнаруженных ключевых точек:», len (ключевые точки))
xfeatures2d.SURF_create (500)
ключевых точек, дескрипторы = surf.detectAndCompute (серый, нет)
print («Количество обнаруженных ключевых точек:», len (ключевые точки))  FastFeatureDetector_create ()
# Получить ключевые точки, по умолчанию не максимальное подавление включено
# для выключения set fast.setBool ('nonmaxSuppression', False)
ключевых точек = fast.detect (серый, нет)
print («Количество обнаруженных ключевых точек:», len (ключевые точки))
FastFeatureDetector_create ()
# Получить ключевые точки, по умолчанию не максимальное подавление включено
# для выключения set fast.setBool ('nonmaxSuppression', False)
ключевых точек = fast.detect (серый, нет)
print («Количество обнаруженных ключевых точек:», len (ключевые точки)) 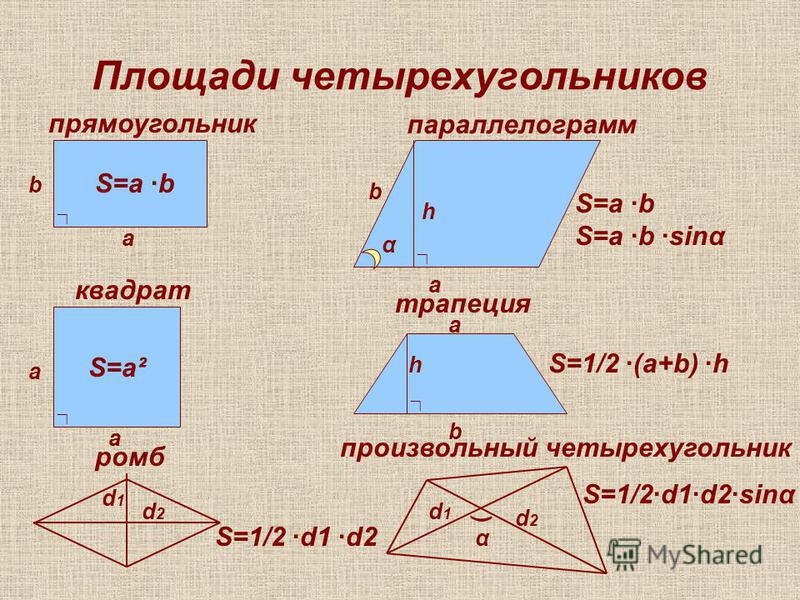 imread ('paris.jpg ')
серый = cv2.cvtColor (изображение, cv2.COLOR_BGR2GRAY)
imread ('paris.jpg ')
серый = cv2.cvtColor (изображение, cv2.COLOR_BGR2GRAY) 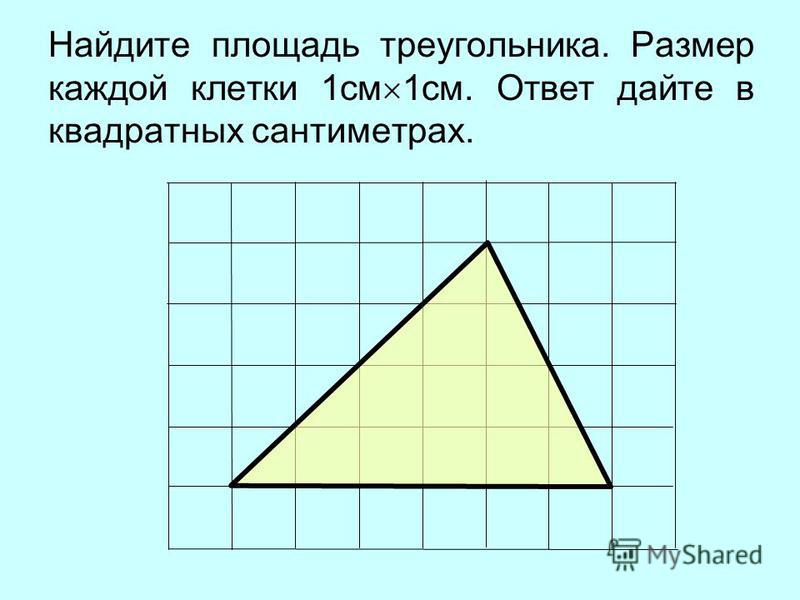 DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
cv2.imshow ('Feature Method - BRIEF', image)
cv2.waitKey ()
cv2.destroyAllWindows ()
DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
cv2.imshow ('Feature Method - BRIEF', image)
cv2.waitKey ()
cv2.destroyAllWindows () 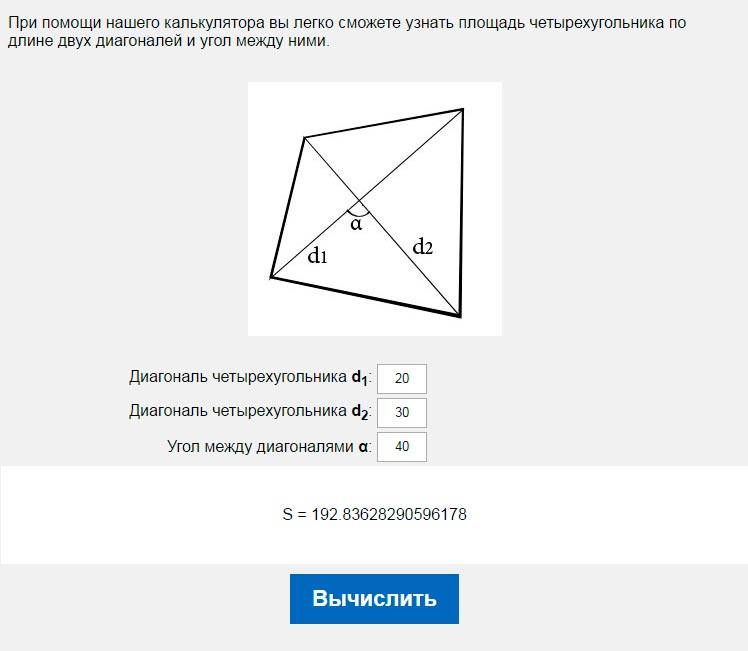 compute (серый, ключевые точки)
print («Количество обнаруженных ключевых точек:», len (ключевые точки))
compute (серый, ключевые точки)
print («Количество обнаруженных ключевых точек:», len (ключевые точки))  : переключено на листовки карт
: переключено на листовки карт .. Пассажирский самолет
.. Пассажирский самолет